Dr. Ashish Karn
Combining two squares having unequal side lengths
For the construction of a fire altar of proper size and shape, it is also necessary to know how to combine into a square figure of other kinds; eg. a square and a rectangle, two rectangles. No specific rule for this purpose is found in the shulbasutras. Figures of every other kind are first transformed into squares and then combined into squares by these methods,
Combining two unequal squares-
Katyayana shubsutra explains the method of construction of a square by adding two unequal squares. It can be stated as,
नानाप्रमाणसमासे ह्र्सीयसः करण्या वर्षीयसोपच्छि न्द्यातत्स्याक्ष्णया रज्जुरुभे समस्यतीति समासः|| कत्यायन शुल्बसुत्रम् २.२२||
“In case of combining the two unequal squares, one should cut off a rectangle from the longer square by aside of the smaller square. The aksnya (diagonal) of this rectangle will combine both the square” (K.S 2.22)
Let ABCD be a larger square and NOPQ a smaller square. Now, cut off a rectangular portion of AEFD from the larger square ABCD such that AE = DF on the side of NOPQ. Draw AF, the diagonal of the rectangle AEFD.
Draw the square AFGH on AF. The area of AFGH will be equal to the combined area of ABCD and NOPQ. This rule is the application of the Baudhayana theorem.
In Katyayana, it is given in the sutra 2.11 as
दीर्घचतुरस्त्रस्याक्ष्णयारज्जुस्तिर्यङ्मानी पार्श्वमानी च यत्पृथग्भूतेकुरुतस्तदुभयं करोतीति क्षेत्रज्ञानम्||२.११||
“In an oblong, its akshnya(diagonal) produces by itself both the areas which the tiryanmani( width) and the parshvamani(length) of the oblong produce separately.(K.S. 2.11)
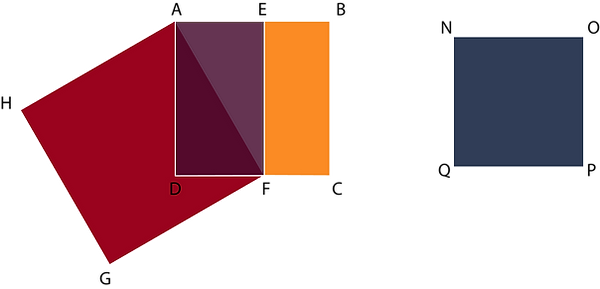
According to this, In a rectangle AEFD,
AF2 = AD2 + DF2.
□ AFGH = □ABCD + □ NOPQ
Computational tool for combining two unequal square,
