Dr. Ashish Karn
Converting a square into a trapezium
The shape of the Ashvamedhiki Vedi, is an isosceles trapezium whose head, foot, and altitude are respectively 24√2 30√2, 36√2 prakramas. The name for the trapezium used by the Shulbasutras is ekatonimat(smaller on one side). Mahavedi, the vedi for soma sacrifices and other vedis were to be in shape of Trapezia. Baudhayana and Apastambha shulbastura give rules for converting square into trapezium.
Baudhayana deals with the problem,
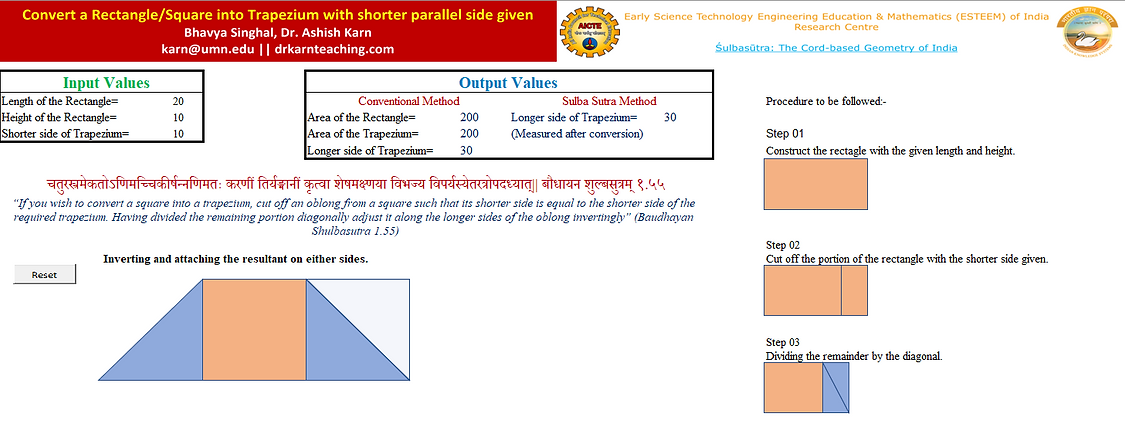
चतुरस्त्रमेकतोऽणिमच्चिकीर्षन्नणिमतः करणीं तिर्यङ्मानीं कृत्वा शेषमक्ष्णया विभज्य विपर्यस्येतरत्रोपदध्यात्|| बौधायन शुल्बसुत्रम् १.५५||
“If you wish to convert a square into a trapezium, cut off an oblong from a square such that its shorter side is equal to the shorter side of the required trapezium. Having divided the remaining portion diagonally adjust it along the longer sides of the oblong invertingly” (B.S. 1.55)
Let ABCD be the given square. Cut off an oblong ABEF from the square such that AF = BE the shorter side of the required trapezium. Divide the remaining portion ECDF by the diagonal DE. Adjust DEC to the north of ABEF by inverting its position. The resultant figure BEDG is the required trapezium.

Satapatha Brahmana also gives a method of conversion of square into trapezium,
चतुर्विंशत्यंगुलिभिर्मिमीते| चतुर्विंशत्यक्षरा वै गायत्री, गायत्रोऽग्निर्यावानग्निर्यावत्यस्य मात्रा तावतैर्वनं तान्मिमीते| स चतुरङ्गुलमेव उभयतोऽन्तरत उपसमुहति, तावद् व्यदूहति| तब्राहेवातिरेचयति नो कनीयः करोति||
“ He measure by 24 angulis. For Gayatri has 24 letters and agni is of gayatri. As much as is the agni, as much as is its measure, by that much he measures them. He contracts 4 angulis inwards on both sides. As much as he contracts, so much he stretches. Thus he does not make it exceed (the right measure) nor does he make it smaller”.
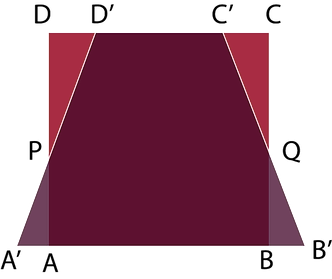
Dutta explains it as the face square (ABCD) is shortened on the either side by the same length to A' and B' .Then, the area of trapezium A 'B'C'D' = the area of square ABCD, Since triangle PDD' = triangle PAA'
and triangle QCC' = triangle QBB'. This methods reappears in the Apastambha Shulbasutra.